A. R. Thompson
July 9, 1998
Digital samples with three or more bits per sample (eight or more quantization levels) have been suggested as a possible format for IF signals that would be digitally filtered before input to the delays and correlator of the MMA. Since such signals would have to be truncated to no more than four levels before entering the correlator, use of more levels in the initial quantization would keep the overall loss of sensitivity similar to that for a single quantization without subsequent truncation. For consideration of such a scheme it is necessary to know the quantization efficiency factors for the larger numbers of levels, that is, the fractions by which the signal-to-noise ratio at the correlator output is degraded by the quantization. The quantization efficiencies for two, three, and four levels have been calculated by a number of authors: see e.g. Cooper (1970), Hagen and Farley (1973) or the review of methods and results in Thompson et al. (1986). These methods involve calculation of the mean and mean-squared outputs of the correlator and become somewhat cumbersome when applied to larger numbers of levels. This memorandum explores the possibility of using a simpler approximation for cases where the number of levels is large, and consequently the loss in sensitivity is small. The principle of the method is to calculate the fractional increase in the variance of a signal that results from the quantization. The signal-to-noise ratio at the correlator output is inversely proportional to this variance.
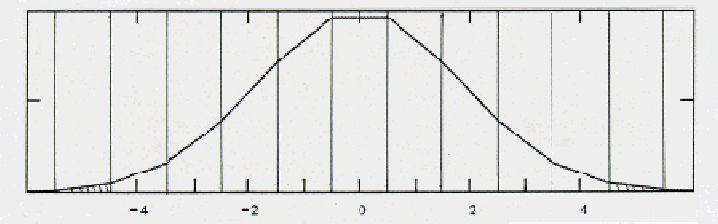
Figure 1. A representation of the Gaussian probability distribution of amplitude of the IF signal, with quantization thresholds for nine-level sampling shown by the vertical lines. The figures along the bottom indicate the digitized levels (weights) assigned to the signals that fall within the corresponding levels. The width of each quantization level is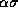 
within the range 
1/4 of signal voltage. Signal levels outside of this range fall within the small shaded areas under the curve and are assigned quantized values of -4 or +4.
Figure 1 shows a piecewise-linear approximation of the Gaussian probability distribution of a signal from one antenna. This approximation simplifies the mathematics without significantly degrading the results. Quantization thresholds for nine-level representation of the signal are indicated by the vertical lines. The widths of the levels are 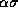in voltage, that is, 
in units of 
where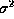 
is the unquantized variance. We consider here the case where the number of levels is odd, and the central level is centered on zero volts. The probability that any one sample will fall between the two consecutive thresholds at 
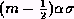and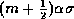 
, where m is an integer, is
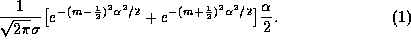
Consider, for example, the level for which m=3. Any voltage that falls within this level is encoded as amplitude 3, although it can be anywhere between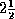 
and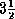 
in units of 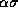. The mean increase in the variance resulting from this representation is
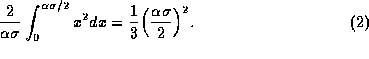
Note that this is exact for the piecewise-linear probability curve in Fig. 1. The same increase in variance resulting from quantization applies to the range of signal levels from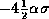 
to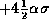 
. The fraction of the area under the Gaussian probability curve that lies between these levels is
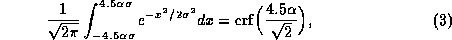
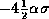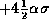Thus the variance resulting from quantization for signals between to is
We shall assume that the quantization error is essentially uncorrelated with the unquantized signal. In the extreme case of two-level sampling the quantization error is essentially the same as the unquantized signal, so the treatment used here would not apply. Consider, however, the case of multilevel quantization as in Fig. 1. If the signal voltage is increased steadily, the quantization error decreases from a maximum at each quantization threshold to zero when the voltage is equal to the mid point of two thresholds. At each threshold the quantization error changes sign and the cycle repeats. This behaviour effectively destroys any correlation between the quantization error and the signal waveform.
It is also necessary to take account of the effect of counting all signals below 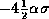as level -4, and those above 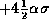as +4. To make an approximate estimate of this effect we divide the range of signal level outside of 
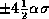into intervals of width 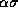. Consider, for example, the interval centered on 
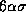. The probability of the signal falling within this level is equal to the corresponding area under the curve, which for the piecewise-linear approximation is
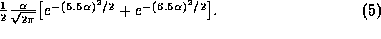
The square of the mean error resulting from quantization of the signal within this range is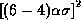 
, so the total variance of the quantization error for signals outside the range 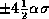is
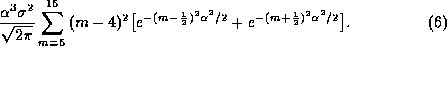
The upper limit of the summation in (6) is chosen to be large enough that increasing it does not significantly change the result. The quantization error resulting from the truncation of the signal values outside the range 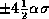clearly has some degree of correlation with the unquantized signal level. However, this is not large because the fraction of samples for which the signal lies outside 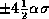is less than 
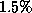for nine-level quantization, and decreases as the number of quantization levels increases. We shall therefore treat the quantization error resulting from the truncation of the signal peaks as uncorrelated with the signal, but bear in mind that this assumption may introduce a small uncertainty into the calculation.
The variance of the quantized signal is equal to the variance of the unquantized signal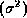 
plus the variance of the quantization errors in (4) and (6), that is,
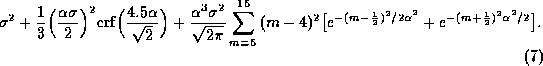
If the variance is the same for both signals at the correlator input, and if the correlation of the two signals is small, the signal-to-noise ratio at the correlator output is inversely proportional to the variance. Thus the quantization efficiency factor is
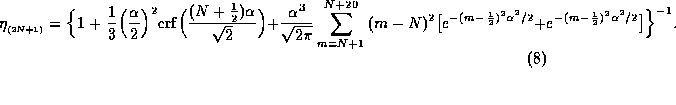
Here the equation has been generalized for for 2N+1 levels. The result from Eq. (8) for nine-level quantization is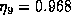 
for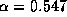 
. The value of was chosen to maximize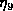 
. These values can be compared with results for nine-level quantization computed by F. R. Schwab using the more precise methods mentioned above. For nine levels this involves evaluation of 
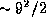probability integrals. Schwab obtained 
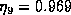for 
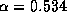. The quantization efficiency varies only slowly with , and the difference in the two values above makes no significant change in 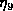. The value of 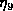from Eq. (8) agrees with the value obtained by Schwab to within 
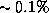, or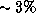 
in the degradation factor 
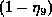. This agreement verifies the present method within these limits of accuracy.
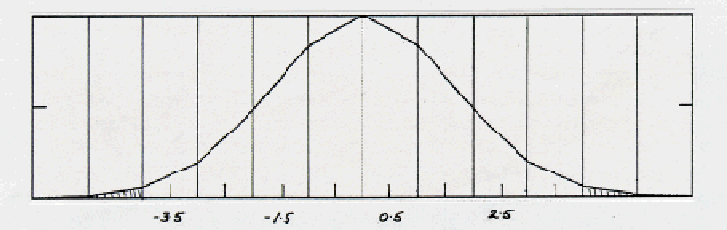
Figure 2. Representation of the Gaussian probability distribution of the amplitude of the IF signal, as in Fig. 1, but for an even number of quantization levels (eight shown in the figure). The quantization thresholds are shown by the vertical lines, and the zero level for signal input coincides with the central threshold, rather than with the center of a level as in Fig. 1. Again the figures along the bottom indicate the digitized levels (weights) assigned to the signals in that fall within the corresponding levels. In this case there is no zero level. Signal levels outside the range 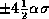fall within the the shaded areas.
For quantization with an even number of levels, as shown in Fig. 2, the central threshold level is at zero signal volts, and the the expression for the quantization efficiency is
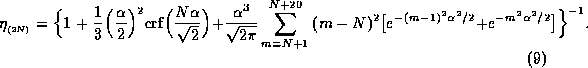
Results from Eqs. (8) and (9), evaluated using Mathcad, are given in Table 1 for 8, 9, 16, and 32 levels.
The second column of Table 1 gives the value of N which indicates the range of quantized values. The third column of the Table gives P, which is the fraction of samples for which the signal amplitude is greater than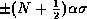 
for odd numbers of levels or greater than 
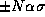for even numbers of levels. P is the fraction of signal samples that contribute to the variance in (6). The values of P are less than 1.6% in all cases listed in Table 1, and decrease as the number of levels increases.
With values of quantization efficiency approaching unity other effects, such as the departure of the bandpass responses from the ideal rectangular shape, become limiting factors. These should be borne in mind if the absolute value for 
is critical. An interesting point about the treatment here is that it shows the connection between the quantization efficiency and the quantization errors rather more clearly than other methods.
Thanks are due to F. Schwab for permission to quote his unpublished results and for discussion of the memorandum in draft.
Cooper, B.F.C., Correlators with Two Bit Quantization, Aust. J. Phys.23, 521- 527, 1970.
Hagen, J.B. and D.T. Farley, Digital Correlation Techniques in Radio Science, Radio Sci., 8, 775 - 784, 1973
Thompson, A.R., J.M.Moran, and G.W. Swenson, Interferometry and Synthesis in Radio Astronomy. Wiley, NY, 1986, and reprinted by Kreiger, Malabar, FL, 1991, 1994. (see Ch. 8)