Adrian Webster
Royal Observatory Edinburgh, Scotland
October 13, 1998
A design for the intermediate configurations of the MMA is presented in which the stations are distributed in a circularly-symmetrical fashion about the centre of the array, with the density of stations dropping as the inverse square of the distance from the centre. There are no fixed configurations within this distribution, and instead a scheme is presented in which the antennas are sited at any given time on an annular region between an inner radius b and an outer radius a. There are many such annuli possible, with different average radii, so the telescope has a `zoom' property in that the antennas can be placed so as to give a synthesised beam whose width may be set to within about one percent of any desired value in the appropriate range. The sidelobe levels in snapshot mode and the ratio of longest instantaneous baseline to shortest are investigated and found to improve as the ratio a/b is increased; for values of the ratio greater than 4 these properties are excellent, and better than those of rings or other configurations that have been considered for the MMA.
One of the most important planning decisions for the MMA is how to site the stations for the antennas. Discussions of this issue are often based on the idea that there will be a small number of configurations, possibly four (e.g. Holdaway 1998, Kogan 1998b, Helfer & Holdaway 1998a), each with its own particular design criteria and its own particular layout, and that at any given time observations will be made with all the antennas situated on just one of the configurations. At present the criteria for two of these configurations (namely the smallest and the largest) are more or less decided and the designs are therefore becoming clear. The smallest configuration is required to give the closest possible approximation to a filled aperture in order to map large-scale sources with the highest possible sensitivity, and so the antennas are likely to be sited within a circle on a `crystalline' close-packed hexagonal lattice in which the antennas are placed as close to each other as possible. The largest configuration, on the other hand, is required to provide the greatest possible number of long baselines for the resolution of the most compact sources, and will probably consist of a ring array, with the antennas sited close to the circumference of a circle or a Reuleaux triangle.
It is less clear at this stage, however, what form the intermediate configurations will take, partly because there is less agreement on what the appropriate design criteria should be. Here the possibilities are discussed and one approach is developed that appears to show particular promise.
It is supposed from the outset that there are three important considerations guiding the design of the intermediate configurations. The first is that these configurations, particularly the smaller ones amongst them, will often be used in snapshot mode and should therefore have instantaneous beam profiles of high quality, with low sidelobe levels. The second is that it should be possible to site the antennas on the stations in such as way that the width of the synthesised beam will be acceptably close to any predetermined value in the appropriate range. The third is that the instantaneous uv-plane distribution should possess plenty of short spacings and should lack undesirable features such as a large central hole, in order that maps of sources of moderate extent may be made with wide dynamic range in just one observation without the need to combine measurements made at different times when the array is in two or more different configurations.
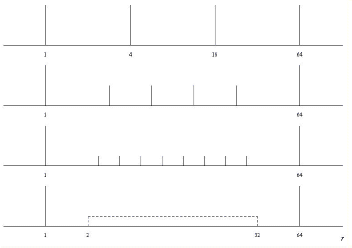
The first model considered here for the layout is a very simple one: it consists of four concentric configurations, each of which is ring-like, with the ratio of the diameters of consecutive configurations equal to 4 (Fig. 1). This model is not particularly realistic because the innermost configuration of the MMA is unlikely to have the form of a ring and because the ratio of successive diameters may be closer to 3.5 than to the round number 4, but it does serve to start the discussion. The first point to note is that rings have high sidelobe levels and are therefore not very suitable for making snapshots. The second is that at any given wavelength the beams of the consecutive configurations differ by a factor 4 and therefore need not match closely the beamwidth regarded by an observer as ideal for any particular source. The worst case occurs when the desired beamwidth falls at the geometric mean of the beamwidths of two consecutive configurations, because the closest available beams are then either a factor of 2 too wide or a factor of 2 too narrow, and such a degree of mismatch is inconveniently large. The mismatch may be reduced by a large factor by hybridization, that is by transferring some of the antennas from the stations of one configuration and onto those of the next, because the beamwidth only changes by a small amount for each antenna transferred; the beam profiles for hybrids consisting of concentric circular configurations are given in Fig. 2 where, unfortunately, the sidelobe levels may be seen to be of the order of 10 - 20%, which is too high to be acceptable for snapshots. The sidelobe levels could probably be reduced by designing the rings in the shape of Reuleaux triangles rather than circles (Webster 1998), but the likely improvement is small.

Another way to reduce the mismatch is by making more configurations available.
If, for example, the existing rings were deleted and replaced by twice as many
rings, as shown in the second panel of Fig. 1,
the beamwidth would change from configuration to configuration by
a factor of two and the greatest mismatch would be by only a factor of
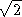 , a substantial improvement.
There would be a cost, however, if each of the rings were to consist of
, a substantial improvement.
There would be a cost, however, if each of the rings were to consist of 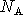 stations (where
stations (where 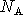 is the number of antennas),
because twice as many stations would be required, and
it is therefore supposed instead that each ring only consists of NA/2,
which leaves the total number unchanged.
It is no longer possible to place all the antennas on one ring and so the observing
configurations consist of pairs of consecutive rings,
but the ratio of the beamwidths of successive configurations is still 2.
These pairs of rings are `thick rings' and their sidelobe levels are expected
from previous studies (Kogan 1998a) to be lower than those of thin rings,
but the beam profiles are not calculated here
because it is more interesting to explore the consequences
of repeatedly doubling the number of rings
whilst halving the number of stations on each (Fig. 1).
This is supposed to be done so many times that the discrete nature of the rings
may be neglected and the ring model replaced by a continuum model.
is the number of antennas),
because twice as many stations would be required, and
it is therefore supposed instead that each ring only consists of NA/2,
which leaves the total number unchanged.
It is no longer possible to place all the antennas on one ring and so the observing
configurations consist of pairs of consecutive rings,
but the ratio of the beamwidths of successive configurations is still 2.
These pairs of rings are `thick rings' and their sidelobe levels are expected
from previous studies (Kogan 1998a) to be lower than those of thin rings,
but the beam profiles are not calculated here
because it is more interesting to explore the consequences
of repeatedly doubling the number of rings
whilst halving the number of stations on each (Fig. 1).
This is supposed to be done so many times that the discrete nature of the rings
may be neglected and the ring model replaced by a continuum model.
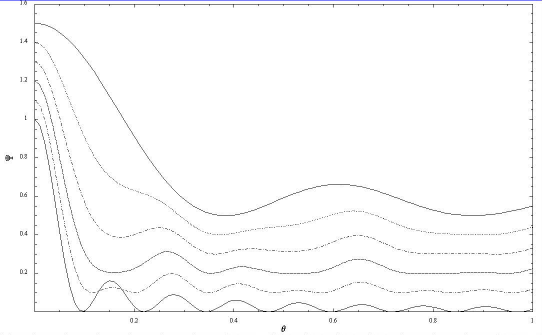
Figure 2:
The beam profiles of hybrids consisting of two concentric rings of antennas, the
outer with 4 times the diameter of the inner. The top curve is the profile
when all the antennas are on the inner ring, the next when 20% of the antennas
are on the outer, then 40, 60 80 and finally 100%.
Successive curves are displaced vertically for clarity.
In the continuum model the distribution of stations on the ground is represented by
a continuous function of the coordinates 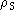 .
One way of regarding this function is as an approximation corresponding to
the limit of the above process, and another
is as an underlying probability distribution, with any particular
arrangement of a finite number of antennas that conforms to the distribution
being regarded as a realization of a statistical process based on that probability
distribution.
The continuum approach has the advantage of distinguishing those features of
the synthesised beam that are fundamental to the underlying distribution from
those that are a consequence of the particular disposition of the finite
number of real antennas, that might be improved by choosing a different
disposition based on the same
.
One way of regarding this function is as an approximation corresponding to
the limit of the above process, and another
is as an underlying probability distribution, with any particular
arrangement of a finite number of antennas that conforms to the distribution
being regarded as a realization of a statistical process based on that probability
distribution.
The continuum approach has the advantage of distinguishing those features of
the synthesised beam that are fundamental to the underlying distribution from
those that are a consequence of the particular disposition of the finite
number of real antennas, that might be improved by choosing a different
disposition based on the same 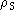 .
Another advantage of the approach is that the synthesised beam profile
can be very easy to calculate.
.
Another advantage of the approach is that the synthesised beam profile
can be very easy to calculate.
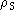 is a continuum density giving the number of stations per square metre.
Attention is limited here to array designs that have circular symmetry about a centre,
so
is a continuum density giving the number of stations per square metre.
Attention is limited here to array designs that have circular symmetry about a centre,
so 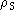 is a function only of the radial distance r
from that centre.
is a function only of the radial distance r
from that centre.
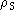 is also taken to have an inverse square law dependence on the distance from the centre of the array:
is also taken to have an inverse square law dependence on the distance from the centre of the array:
where 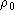 is a dimensionless constant;
this corresponds to the same average scaling of the number of antennas with
radius as the four-configuration array taken as the starting-point of the design
(see Fig. 1).
The stations are taken to be distributed between a minimum radius rmin
and a maximum radius rmax, so the number of stations is
is a dimensionless constant;
this corresponds to the same average scaling of the number of antennas with
radius as the four-configuration array taken as the starting-point of the design
(see Fig. 1).
The stations are taken to be distributed between a minimum radius rmin
and a maximum radius rmax, so the number of stations is
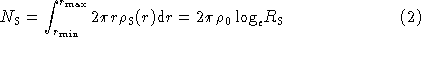
Where 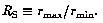 For the continuum model in Fig. 1,
rmin=2, rmax=32, and RS = 16.
For the continuum model in Fig. 1,
rmin=2, rmax=32, and RS = 16.
It is also supposed that there exists a second continuum density 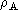 which gives the number of antennas per square metre.
Since the antennas may be moved around,
which gives the number of antennas per square metre.
Since the antennas may be moved around, 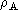 is under
the control of the observatory manager whereas
is under
the control of the observatory manager whereas 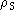 is fixed once the telescope is designed and built.
There are two obvious conditions on
is fixed once the telescope is designed and built.
There are two obvious conditions on 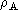 :
there cannot locally be more antennas
than stations,
:
there cannot locally be more antennas
than stations,
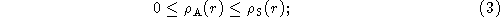
and the density of antennas integrated over the area over which they are distributed must equal the total number of antennas
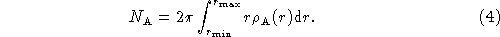
It has been supposed for simplicity that is circularly symmetric (although this condition could later be relaxed when designing, for example, a layout that would give a circular beam at a declination far from the zenith).
With these conditions, the profile of the synthesised beam is readily
calculated as the square of the Hankel transform of 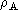 (Bracewell 1965):
(Bracewell 1965):
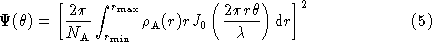
where 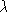 is the wavelength of observation and
is the wavelength of observation and 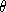 is the angle from
the beam centre in radians.
The constant multiplying the integral has been chosen to give unit forward gain
is the angle from
the beam centre in radians.
The constant multiplying the integral has been chosen to give unit forward gain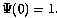 .
.
There is still considerable freedom of choice in the functional form of
A particularly simple form is that based on a distribution of antennas termed
here the `solid annulus', in which
two conditions are both met:
first, all the antennas are sited between an inner radius b and an outer radius a;
and second, there are no unoccupied stations between these radii.
The density of antennas is therefore given by
![]()
(see Fig. 3).
The number of antennas between b and a is
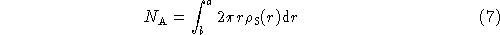
which evaluates to
where 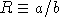 is termed the annular ratio.
This ratio R is an invariant of the array:
its value does not depend on either a or b individually,
but only on the constants NA and
is termed the annular ratio.
This ratio R is an invariant of the array:
its value does not depend on either a or b individually,
but only on the constants NA and  ,
both of which are fixed once the array is built.
Another way of stating r this is that the various solid annuli are self-similar.
,
both of which are fixed once the array is built.
Another way of stating r this is that the various solid annuli are self-similar.
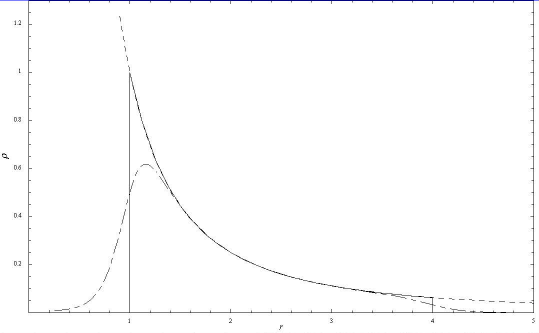
Figure 3:
Annular distributions of antennas. The dashed curve gives 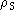 for
the inverse-square law density of stations.
The other curves give the density of antennas
for
the inverse-square law density of stations.
The other curves give the density of antennas 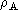 for a
solid annulus (solid line) and a fuzzy annulus (dash-dot line).
for a
solid annulus (solid line) and a fuzzy annulus (dash-dot line).
In an array built of set configurations each configuration consists of NA stations, so it is convenient to define the ratio

as the equivalent number of configurations in the inverse-square part of the array.
For the continuum model in Fig. 1,
in which the inverse-square part was derived from two configurations while
maintaining constant the number of stations, 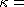 2.
2.
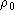 may be eliminated between Eqs. 2 and 8 to give a simple relationship between RS, R, and
may be eliminated between Eqs. 2 and 8 to give a simple relationship between RS, R, and  :
:

For any given value of R,
the beamwidth of a solid annulus scales as the ratio of the wavelength to
some characteristic dimension of the annulus, e.g 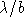 .
Normalized to this dimensionless variable,
the beam profile is a function only of R.
Beam profiles with R in the range from
2 to 8 are plotted in Fig. 4,
where they are seen to consist of a strong forward beam in the form of a clean, bell-shaped curve,
together with relatively weak sidelobes.
The normalization adopted for these plots was to keep the inner radius of the
annulus constant at b=1 while the outer radius was varied as a=R,
so the longest baseline increases with R and as a result
the forward beam becomes narrower as R is increased in this particular presentation.
.
Normalized to this dimensionless variable,
the beam profile is a function only of R.
Beam profiles with R in the range from
2 to 8 are plotted in Fig. 4,
where they are seen to consist of a strong forward beam in the form of a clean, bell-shaped curve,
together with relatively weak sidelobes.
The normalization adopted for these plots was to keep the inner radius of the
annulus constant at b=1 while the outer radius was varied as a=R,
so the longest baseline increases with R and as a result
the forward beam becomes narrower as R is increased in this particular presentation.
In order to investigate the sidelobes,
the same profiles are plotted in Fig. 5 on an expanded vertical scale.
The position and strength of the strongest sidelobe seen in each part of the figure
is given in Table 1 as a percentage of the forward gain.
As R is varied, the position of the strongest lobe varies
somewhat erratically between 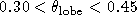 ,
but its intensity declines monotonically
and for
,
but its intensity declines monotonically
and for 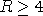 the intensity is of order 1% of the main beam.
the intensity is of order 1% of the main beam.
If solid annuli with different values of R are to be compared,
it would be expected that the half-power beamwidth at any particular wavelength
is determined by 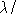
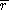 ,
where
,
where 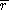 is an appropriate average radius for the annulus,
is an appropriate average radius for the annulus,
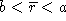 .
It is not, however, immediately obvious which average is appropriate.
.
It is not, however, immediately obvious which average is appropriate.
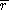
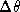 ,
the product of the correct average and the beamwidth at any given wavelength,
should be constant, independent of R,
so three
,
the product of the correct average and the beamwidth at any given wavelength,
should be constant, independent of R,
so three
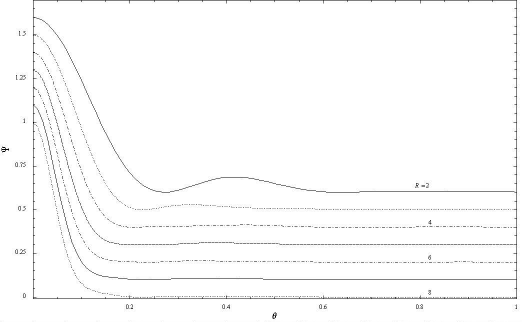
Table 1: The strongest sidelobes of solid annuli as R
is varied.

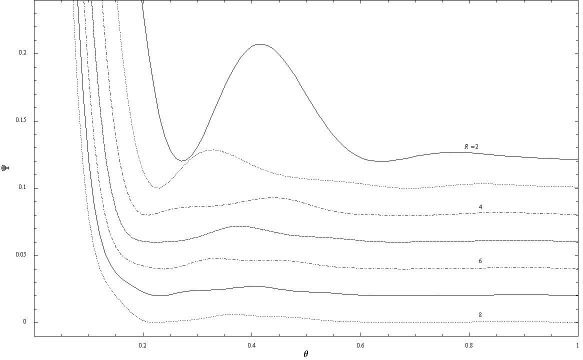
Figure 5: Beam profiles for solid annuli. The
curves are identical to those in the previous figure,
but the vertical scale is expanded.
Figure 6: The product of the average radius of the
annulus, 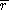 , and the beamwidth to half
maximum,
, and the beamwidth to half
maximum, 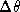 , as a function of R.
The product is normalised to the value of the product for
a thin annulus (i.e. one with R = 1).
, as a function of R.
The product is normalised to the value of the product for
a thin annulus (i.e. one with R = 1).
curves for this product are drawn in Fig. 6,
one for the arithmetic mean 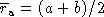 ,
one for the geometric mean
,
one for the geometric mean
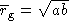 and
one for the mean weighted by
and
one for the mean weighted by 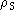 ,
,  .
It may be seen that none of these products is independent of R,
and so the correct average has some other form which is not determined here.
Instead, it may be noted that
the product with the weighted mean varies least,
and so the beamwidth (FWHM) is best given by the empirical formula
.
It may be seen that none of these products is independent of R,
and so the correct average has some other form which is not determined here.
Instead, it may be noted that
the product with the weighted mean varies least,
and so the beamwidth (FWHM) is best given by the empirical formula
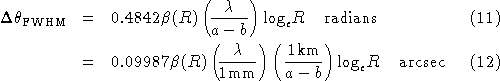
where 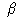 is a slowly-varying function of R.
For many purposes the constant value
is a slowly-varying function of R.
For many purposes the constant value 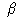 = 0.95
will be found adequate:
over the range
= 0.95
will be found adequate:
over the range 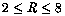 it gives results accurate to a few
percent,
but for purposes requiring more accuracy
it gives results accurate to a few
percent,
but for purposes requiring more accuracy
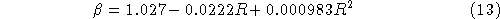
obtained by fitting to the values of the product 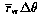 in Fig. 6
gives results to better than 0.1% over the same range.
in Fig. 6
gives results to better than 0.1% over the same range.
Another matter of interest is the ratio of the longest baseline
to the shortest because,
as explained at the start of section 2, this ratio should be as large as
possible in order to provide maps of sources containing structure on a variety
of scales in a single observation.
The lengths of the longest baselines in a solid annulus are of order 2a,
whereas those of the shortest
are of order 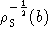 ,
the typical separation of nearest-neighbour stations at the inner edge
of the annulus at r=b, where the density of antennas is highest,
and the ratio of these baseline lengths
,
the typical separation of nearest-neighbour stations at the inner edge
of the annulus at r=b, where the density of antennas is highest,
and the ratio of these baseline lengths
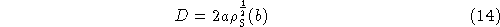
should ideally be as large as possible.
For a given number of antennas NA,
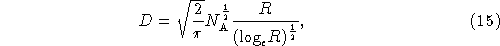
where use has been made of equations 1 and 8.
As may be seen from this equation and Fig. 7,
D increases almost linearly with R, and so
this aspect of the quality of the imaging improves quite fast as R increases.
D also increases as the square root of NA, and so the quality
improves as the number of antennas is increased.
The smallest increase in the average size of a solid annulus
that it is possible to make is achieved by
taking the innermost antenna from r=b and moving it so that it
becomes the outermost by siting it on the first available station beyond
r=a.
This increases the average diameter of the antenna array by a multiplicative factor
that is a little greater than unity, which we term here the quantum of resolution.
The factor need not be the same for each antenna move because
it depends on the exact distribution of stations,
but the average value may be written Q where Q=(1+q), defining
the small quantity q.
Repeating the process of enlargement NA times increases the
size of the annulus by a factor R so
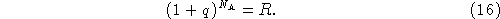
Taking logarithms and approximating 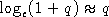 gives
gives
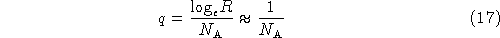
which is of the order of a few percent for the numbers of antennas under consideration for the next generation of millimetre arrays. It is therefore seen that the beamwidths of the solid annuli may be controlled very finely. The astronomer will not often be able to specify in advance the ideal beamwidth of any particular observation with an accuracy as high as that given in the equation, so for many purposes the finiteness of the quantum may be ignored and the array may be regarded as having a zoom property in which the control of the beamwidth is effectively perfect.
The zoom range Z is defined as the ratio of the sizes of the largest
and smallest solid annuli that it is possible to deploy on the
stations of the inverse-square part of the array.
The inside edge of the smallest solid annulus has a radius rmin whereas that of the largest has a radius rmax/R
, so evidently
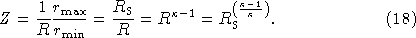
The zoom range therefore increases with R, with RS, and with  . For the model in Fig. 1, Z=4.
. For the model in Fig. 1, Z=4.
All the properties of solid annuli discussed above depend on the annular ratio R,
and here the results are discussed from the point of view of the quality
of the observations that might be made, in order to find what range of
values of R would provide the best telescope.
As R is increased it has been found that
the sidelobe levels decrease monotonically,
the ratio of longest to shortest baseline increases,
and so does the zoom range for a given  .
All of these properties therefore improve as R is increased, because
low sidelobes, a large range of baselines and a large zoom range are
all regarded as desirable.
The only property which degrades as R is increased is the quantum of resolution,
which should ideally be as small as possible,
but q increases with R (equation 17);
it only increases as logeR
so the increase is very slow
and since the quantum is more than small enough for most purposes this
factor is the least important of those discussed here.
When all these matters are taken into account,
it is concluded that large values of R are better than small.
.
All of these properties therefore improve as R is increased, because
low sidelobes, a large range of baselines and a large zoom range are
all regarded as desirable.
The only property which degrades as R is increased is the quantum of resolution,
which should ideally be as small as possible,
but q increases with R (equation 17);
it only increases as logeR
so the increase is very slow
and since the quantum is more than small enough for most purposes this
factor is the least important of those discussed here.
When all these matters are taken into account,
it is concluded that large values of R are better than small.
The solid annulus is not the only way of arranging the
antennas on the stations of the inverse-square distribution,
but it has been found to possess a remarkably good beam profile,
with a simple peak in the forward direction and low sidelobe levels.
It is also a convenient choice
in so far as there is no ambiguity when translating a design based on the
continuum model into a real array with a finite number of stations and
dishes.
Such an ambiguity is met in arrangements in which values of 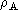 intermediate between 0 and
intermediate between 0 and 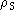 are possible because
a decision then has to be made between the different ways of approximating
such fractional coverage by siting antennas on some of the stations
in a given locality while leaving others empty.
are possible because
a decision then has to be made between the different ways of approximating
such fractional coverage by siting antennas on some of the stations
in a given locality while leaving others empty.
One reason for contemplating an arrangement different from a solid annulus is to reduce the sidelobes still further, but this has not been considered here partly because the sidelobes are already low and partly because the effect of approximating a solid annulus with a finite number of antennas has not yet been investigated. This latter point is of importance because the sidelobe level of a real distribution of a finite number of antennas is inevitably greater than that of the corresponding solid annulus in the continuum model, and if it is much greater there is little point in refining the model further.
A second reason would be to improve the control of the beamwidth. The smallest change of size of a solid annulus corresponds to moving an antenna from the inner radius to the outer, but when there are vacant sites available within the annulus, as for the `fuzzy' annulus sketched in Fig. 7 or for a filled disc-like configuration, shorter moves are possible which alter the beamwidth by a smaller factor. Indeed, it is possible in such cases to envisage moving several antennas, some of them inwards and some of them outwards, in order to control the beamwidth very finely, and it seems likely that the beamwidth could be controlled with at least a factor of ten more precision in this way than is possible with solid annuli.
A third reason is that would also be possible to control the entire beam profile
very finely in this way,
and not just the beamwidth,
and this property could be useful in making scaled array measurements of a given
astronomical object in two different spectral lines because it is sometimes desirable
to observe with beams as nearly identical as possible at the two wavelengths
involved.
For a few cases in which the wavelengths are in the ratio of small integers,
such as the 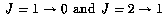 transitions of CO,
it may be possible to design the layout of the stations so that this can be achieved automatically simply by scaling the deployment of the stations in a suitable way (e.g. Conway 1998),
but this is not possible when comparing transitions of different molecules,
such as
transitions of CO,
it may be possible to design the layout of the stations so that this can be achieved automatically simply by scaling the deployment of the stations in a suitable way (e.g. Conway 1998),
but this is not possible when comparing transitions of different molecules,
such as 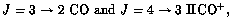 ,
whose wavelengths are not even approximately in the ratio of small integers.
The possibility of controlling the beam profile finely could then enable
this wider class of observations to be made with very similar beam profiles
despite the arbitrariness of the wavelength ratio.
,
whose wavelengths are not even approximately in the ratio of small integers.
The possibility of controlling the beam profile finely could then enable
this wider class of observations to be made with very similar beam profiles
despite the arbitrariness of the wavelength ratio.
It is of interest to compare the properties of solid annuli with two other standard configurations that are often discussed in connection with designs for interferometers, namely an array of antennas distributed uniformly within a disc and a ring array. The former gives an instantaneous uv-plane distribution that is close to Gaussian, and has a first sidelobe level of 1.7%,
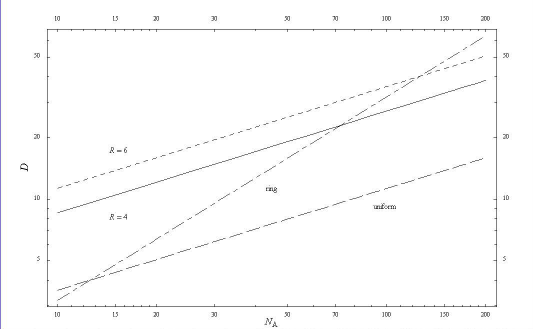
Figure 7: A log-log plot of the ratio of the longest to the
shortest baseline as a function of the number of antennas, for several
types of arrays. Two curves for solid annuli are plotted, as indicated
by the value of R. The other curves are for antennas uniformly
distributed within a circular disc, and for antennas on a ring.
Table 2: The critical value of NA above which ring arrays have a greater ratio than inverse-square arrays of longest baseline to shortest, as a function of R.
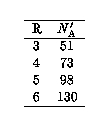
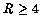 have lower sidelobe
levels than this
(Table 1).
Another mayyer is the ratio of longest to shortest baseline,
which for a uniform disc is
have lower sidelobe
levels than this
(Table 1).
Another mayyer is the ratio of longest to shortest baseline,
which for a uniform disc is
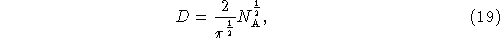
Ring arrays have sidelobe levels an order of magnitude greater than solid annuli, are are therefore much poorer in this respect. Rings can, however, have a large ratio D of the longest to the shortest baseline, and it has been argued that the high sidelobe levels are a minor nuisance compared with the advantage that this ratio brings to mapping complex sources (Helfer & Holdaway 1998b). The ratio of longest to shortest baselines for a ring is

which has has a different dependence on NA than the ratio
for solid annuli (Fig. 7), and if
the number of antennas is greater than some critical value
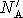 R,
a ring array will have a greater value of D than a solid annulus.
The critical values are given in Table 2, where it
may be seen that for
R,
a ring array will have a greater value of D than a solid annulus.
The critical values are given in Table 2, where it
may be seen that for 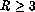 the critical values are high,
and that for
the critical values are high,
and that for 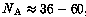 ,
the sort of numbers currently under discussion for the MMA and the MMA + LSA,
the inverse-square arrays are as good as the ring arrays or better
in this regard.
The solid annuli therefore appear to be superior in both respects to rings for
the intermediate configurations of the MMA.
,
the sort of numbers currently under discussion for the MMA and the MMA + LSA,
the inverse-square arrays are as good as the ring arrays or better
in this regard.
The solid annuli therefore appear to be superior in both respects to rings for
the intermediate configurations of the MMA.
One of the main reasons for considering ring arrays at all is that, for a given size, they have a greater number of long baselines than all other known designs, and it of interest to consider whether this property has any value when considering the intermediate configurations of the MMA. If a wavelength is chosen and also a beamwidth corresponding to the intermediate range, then of all possible designs with that beamwidth rings occupy the smallest area of land. It is not at all clear, however, why this property should have any appeal to the observer, particularly when other designs are available that are known to have desirable properties that rings lack, such as ultra-low sidelobe levels or the ability to zoom finely. The large number of long baselines in ring arrays make them ideal for the outer configuration of the MMA, but only the outer, and it seems better to consider other designs for the intermediate configurations.
In this paper, the sidelobe levels, the ratio of longest to shortest baseline, and the ability to zoom have been compared for inverse-square arrays and for rings, and the inverse-square arrays found to be comparable or superior in all respects. It seems, therefore, that serious consideration should be given to abandoning the idea of designing the intermediate part of the telescope in terms of two fixed configurations of ring-like arrays in favour of a `configurationless' design in which the antennas are distributed more widely, because then a large number of useful combinations of stations become available from which astronomical observations of high quality can be made, and a more flexible and powerful telescope should result.
Conway (1998) has suggested a logarithmic spiral design for the intermediate
configurations of the MMA.
The separation between the arms of a logarithmic spiral increases linearly
with the radius r,
and siting the stations at constant increments of azimuth causes
the separation between stations along each arm also to increase linearly with r,
so that overall
the density of stations drops off as the inverse square of r.
The logarithmic spiral is therefore seen to be a particular case of the present designs,
and in terms of the parameters devised in this paper to quantify those designs
the example presented has 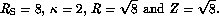
The example has been shown to possess the expected clean beam with low sidelobe levels, the wide range of baseline lengths and the ability to zoom of the more general case discussed here, but it is nevertheless unlikely to be suitable for the MMA because the zoom range is disappointingly small. Z is only about 2.8, so the user of the array would have a choice of beamwidth between the smallest beam from the outer configuration, the largest beam from the most compact, and any beam at all within a narrow intermediate range of about a factor of 2.8. This leaves two wide ranges of beamwidth for which no configuration is available, and so this logarithmic spiral is not as good a choice from this point of view as the four fixed configurations with which the present discussion began (Fig. 1), which might therefore be found preferable. This difficulty is not unavoidable, however, and choosing a larger value of RS would give a wider zoom range, such as the Z=4 of the model in Fig. 1 or the even greater values that may be attained by the designs described in the next section.
With the intermediate configurations of the MMA designed on the inverse-square plan discussed here, the array might be described as a composite, because it would be made up of three completely different sections, each designed to meet different criteria. Although the ability to zoom over the intermediate configuration would be useful, there would still be a gap in the beamwidth coverage between the inner configuration and the intermediate one, and another between the outer configuration and the intermediate.. The width of the gaps could be reduced by extending the intermediate configuration to touch the other two configurations; reducing rmin and increasing rmax in this way would increase RS, R and Z, but it would still not close the gaps completely, which can only be done by hybridization.
It is then very important to discover whether it is possible to design such hybrid composite arrays so that the hybrids have acceptable beam profiles. The inner hybrids are of particular importance in this regard, because they would frequently be used in snapshot mode and must therefore have low sidelobe levels, but it is not obvious from the outset whether hybrids between two such different arrangements as a close-packed hexagonal array and an inverse-square array have acceptable properties. The next paper in this series is an investigation of these matters, with the aim of finding whether it may be possible to produce a design for the MMA that zooms usefully all the way from the most compact to the most extended configuration of the antennas.
The idea has been explored of replacing the intermediate configurations of the MMA with an approximately circularly-symmetrical distribution of stations, in which the spatial density of stations drops as the inverse square of the distance from the centre of the telescope. One particular way of distributing the antennas on these stations was studied, in which all the antennas lie within a concentric circular annulus, and it was found that the properties of the synthesised beam are of remarkably high quality. For a wide range of parameters, the beam profile consists of a clean central peak with low sidelobe levels, and the uv-plane coverage is good, with a wide range of baseline lengths and no central hole or other unwelcome feature. Both of these desirable properties are found to improve as the ratio of the outer radius of the annulus to the inner is increased. The designs also have a useful zoom property: there are many annular arrangements of the antennas possible on the stations of the inverse-square part of the array and it is not difficult to find one that has a beamwidth within one percent or so of any desired value in the appropriate range. Other ways of deploying the antennas on an inverse-square distribution of stations were discussed, and it seems seems likely that there exist configurations with even better properties.
Bracewell R., 1965, The Fourier Transform and its Applications,
McGraw-Hill, London
Helfer T.T. and Holdaway M., 1998a,
Design Concepts for Strawperson Antenna Configurations for the MMA,
MMA Memo Series number 198.
Helfer T.T. and Holdaway M., 1998b,
Chapter 15 of the MMA Project Book,
http://www.tuc.nrao.edu/ demerson/project_book/chap15/chap15.html.
Holdaway M., 1998, MMA Configuration Design Concepts,
http:/www.tuc.nrao.edu/mma/config/config.html
Kogan 1998a, Optimization of an Array Configuration with a Donut Constraint,
MMA Memo Series number 212.
Kogan 1998b,
A, B, C, and D configurations in the shape of concentric circles with fixed pads at the common circumferences, MMA Memo Series number 226.
Webster A.S., 1998, Hybrid arrays: the design of reconfigurable aperture-synthesis interferometers, MMA Memo Series number 214.